はじめに
高性能のモーション制御システムの帰還ループにMEMS(Micro Electro Mechanical Systems)ベースの慣性計測ユニット(IMU)を使用する場合、センサーのミスアライメント(軸の方向のずれ)が重要な検討事項になります。IMUが内蔵されたジャイロスコープにおいて、センサーのミスアライメントは各ジャイロスコープの回転軸と、システムで定義された慣性基準フレーム(グローバル・フレームとも呼ばれます)の間の角度差で表されます。ミスアライメントがセンサーの精度に与える影響を管理するには、製品に固有のパッケージや特殊な組み立てプロセス、最終的な構成(コンフィギュレーション)を踏まえた複雑な慣性テストが必要になるかもしれません。これらのすべてが、プロジェクトを管理するうえでの重要な評価指標に多大な影響を及ぼす可能性があります。ここで言う評価指標とは、スケジュール、投資額、各システムにおけるIMU関連の総コストなどのことです。これらは設計サイクルの初期段階で検討すべき事柄です。センサーのアライメントは、これらの事柄に対する評価指標だと言うこともできます。設計サイクルの初期段階であれば、最も効率的なソリューションを実現可能なシステム・アーキテクチャを定義するための時間を確保することができます。一方、プロジェクトの工程が80%ほど進み、予算の80%を費やした段階になって、全く問題のない製品をエンドユーザーに提供するため、安価なセンサーに数百ドル~数千ドルもの追加コストをかけなければならないと気づいたらどうなるでしょうか。そうした事態は誰もが避けたいと考えるはずです。
システムで使用するIMUの機能を設計する際、アライメントに関する3つの基本的な事柄を理解して評価を行う必要があります。3つの事柄とは、誤差の見積もり、ミスアライメントがシステムの主要な動作に与える影響、(配備後の)電気的なアライメントです。これらのうち、誤差の見積もりについては、IMUと、動作時にそれを支える機械的システムの両方に起因する誤差を考慮する必要があります。また、ミスアライメントがシステムの主要な動作に与える影響について理解すれば、問題に対して過剰な処置を施すことなく目標とする性能を達成することができます。これは、主要な性能とコストの要件を満たすことができない可能性を排除するためのリスク管理にもつながります。また、システムの性能とコストの間のトレードオフを最適化するために、何らかの電気的なアライメントが必要になる場合があります。
配備後のアライメント誤差の予測
アプリケーション全体のアライメントの精度は、IMUのミスアライメント誤差と、動作時にそれを支持する機械的システムの精度という2つの項目に主に依存します。通常、IMUに起因する誤差ΨIMUと機械的システムに起因する誤差ΨSYSは互いに依存しません。トータルのミスアライメント誤差は、2つの誤差の二乗和平方根を計算することで見積もることができます。

IMUのスペックシートでは、ミスアライメント誤差が、軸とパッケージの間、または軸とフレームの間のミスアライメント誤差などのパラメータとして定量化されていることがあります。図1は、アナログ・デバイセズ(ADI)のMEMS慣性センサー「ADIS16485」に内蔵された各ジャイロスコープのパッケージの角からのミスアライメント誤差を誇張して示したものです。この図において、緑色の点線はパッケージによって定義される基準フレームの軸、実線はパッケージ内のジャイロスコープの回転軸をそれぞれ表しています。ΨIMUは3つのミスアライメント成分ΨX、ΨY、ΨZの最大値となります。
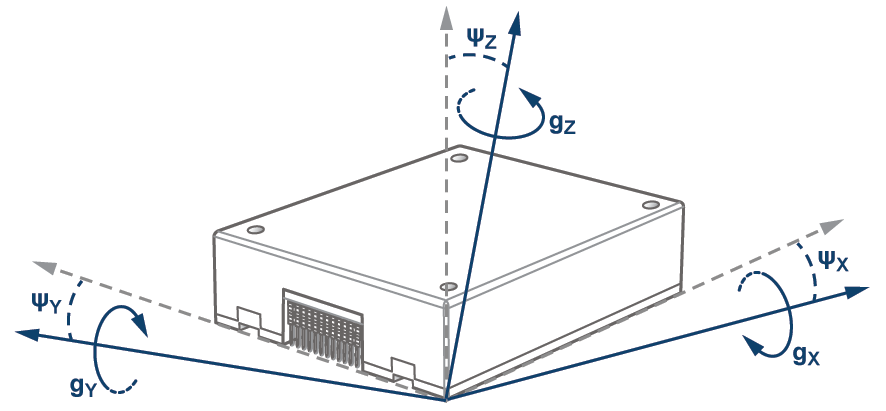
ミスアライメント誤差のうち、システムに起因する誤差(式1のΨSYS)を見積もるには、システムにおいて基準フレームに基づくIMUの配置位置に、スキュー(ゆがみ、傾斜)をもたらす要因となる機械的欠陥が存在する可能性について解析する必要があります。プリント回路基板にはんだ付けされたIMUを使用する場合、もともとの配置精度、はんだの付着量のばらつき、リフロー時のはんだの浮き、プリント基板上の取り付け穴などの形状の許容誤差、システムのフレーム自体の許容誤差などを検討しなければなりません。一方、モジュール・レベルのIMUを使用する場合は、図2に示すように、システムの筐体により直接的に結合できる可能性があります。このように結合する場合、取り付けレッジ(4カ所)と取り付けネストという2つの機械的形状によって、取り付けスキュー誤差を管理することができます。
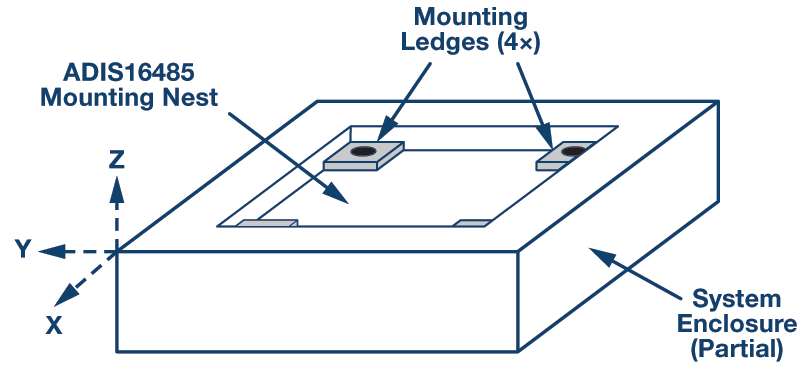
このような取り付け構造において、4つの取り付けレッジの高さのばらつきは、X軸とY軸で取り付けスキューを生じさせる機械的ばらつきの一例となります。図3は、このばらつき(H1とH2の差)がX軸の取り付けスキューΨXに与える影響を示すために、そのスキューを誇張して示したものです。
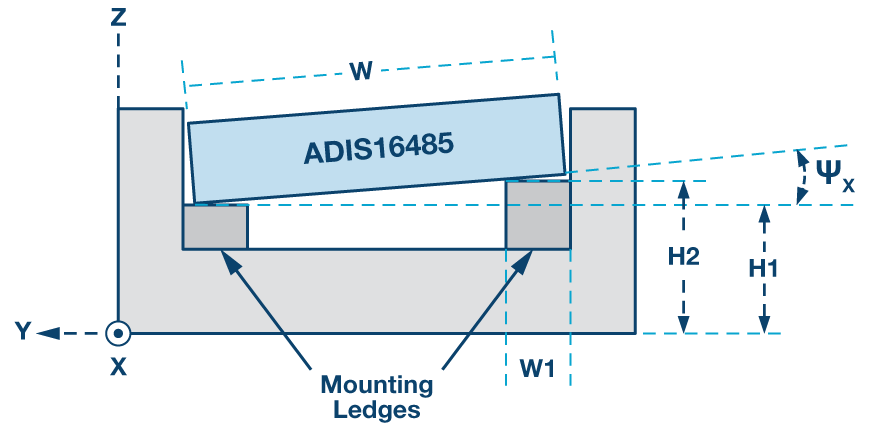
以下に示す式(式2)を使えば、高さの違い(H2とH1の差)と2つの接点間の距離(WとW1の差)によるX軸のスキュー角ΨXを見積もることができます。
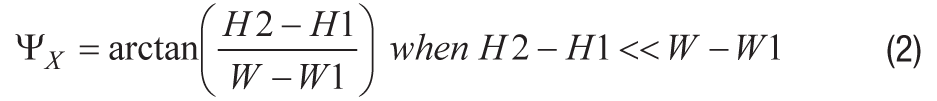
同様に、取り付けレッジの高さのばらつきはY軸の取り付けスキューにも影響を及ぼします。式3は、式2の幅Wをパッケージ長Lで置き換えたものです。この式を使えば、Y軸のスキュー角ΨYを見積もることができます。
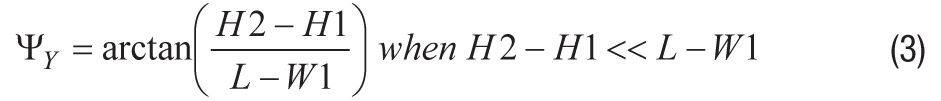
図4は、Z軸の取り付けスキューに機械的属性が影響を与える様子を示したものです。ここで、小ねじはIMU本体の(4隅にある)取り付け穴と、取り付けレッジのスルー・ホールを介して、取り付けレッジ背面のナットで固定されます。図中のDMは小ねじの直径です。また、DHは小ねじに対応するベースプレート上のパススルー・ホールの直径です。DMとDHの差が、Z軸のスキューが生じる要因になります。
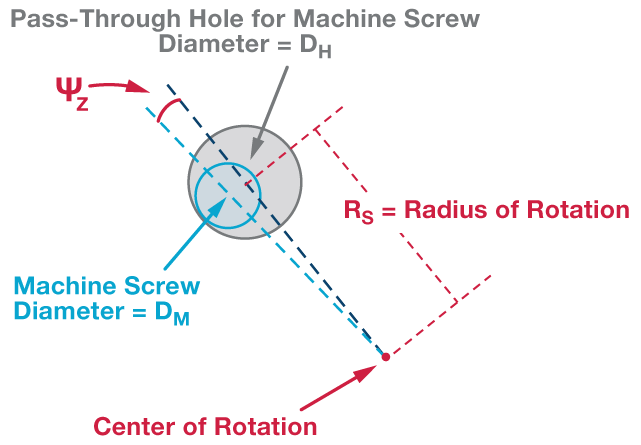
Z軸の取り付けスキューΨZは、この直径の差と回転半径RSに基づき、式4によって見積もることができます。回転半径は、対角にある2つの取り付けねじの間の距離の半分になります。
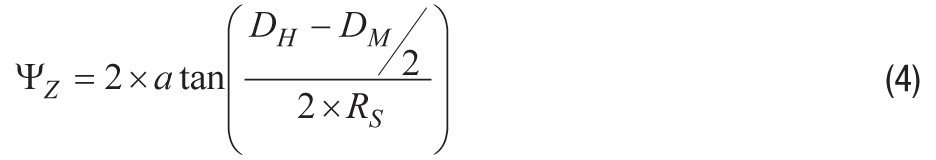
【例題1】
2mmの小ねじを使用し、ADIS16485を6mm×6mmの取り付けレッジに取り付ける場合の全体的なミスアライメントを見積もるにはどうすればよいでしょうか。取り付けレッジの直径は2.85mm、高さの許容誤差は0.2mmです。
【解答】
幅Wの公称値44mmを用いると、X軸のスキュー角の見積もり値(図3参照)は、以下のように0.3°となります。
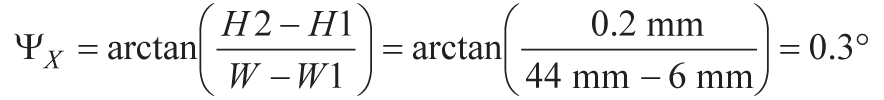
このパッケージの各対辺上にある取り付け穴の間の距離は公称値でそれぞれ39.6mmと42.6mmです。これらの長さを2辺とする直角三角形の斜辺が、パッケージの対角にある2つの穴の間の距離になります。回転半径RS(図4参照)はこの距離の半分(29.1mm)なので、Z軸のスキューの見積もり値は以下のように0.83°となります。
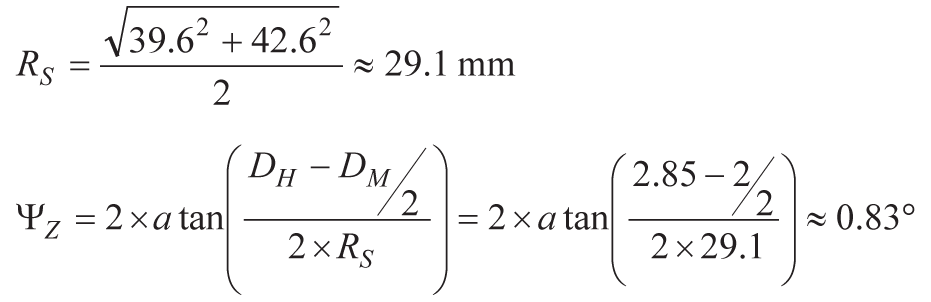
これを式1に対応づけると、ΨSYSはΨZ(予測値の最大値)に等しく、ΨIMUはIMUのデータシートに記載されている軸とフレームの間のミスアライメント誤差の仕様値である1°となります。したがって、総合的なミスアライメント誤差の見積もり値は以下のように1.28°となります。
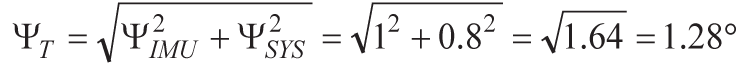
ミスアライメントがシステムの精度に及ぼす影響
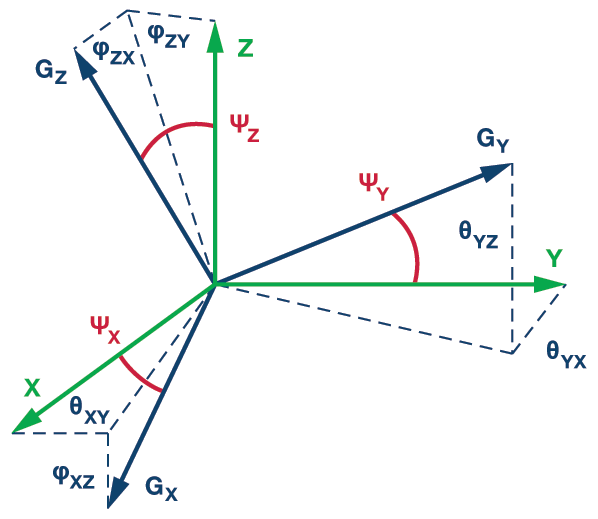
アプリケーションにおける精度の基準を定める際には、ミスアライメント誤差とそれがジャイロスコープの精度に与える影響の基本的な関係を理解しておく必要があります 。3軸ジャイロスコープ・システムの概念を示した図5において、3本の緑色の実線は基準フレームの3軸、黒色の実線は3つのジャイロスコープの回転軸、Ψで始まるラベルは基準フレームとジャイロスコープの軸の間のミスアライメント誤差をそれぞれ表します。式5、6、7は、基準フレームの軸周りの回転に対して、各ジャイロスコープの応答にミスアライメント誤差が与える影響を表します。これらの式から、スケール誤差はミスアライメント角の余弦によって表されることがわかります。

ミスアライメント誤差は各軸間にも影響を及ぼします。この影響を定量化するには、各軸のミスアライメント角度をそれ以外の2軸に関連する2つの成分に分割する必要があります。例えば、ΨXであればY軸成分ΦXYとZ軸成分ΦXZに分割します。この際、基準フレームの3軸ωX、ωY、ωZの回転に対するX軸のジャイロスコープの応答は、次のように拡張されます。
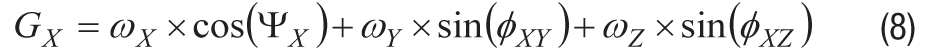
同様に、Y軸とZ軸のジャイロスコープの応答も以下のように拡張されます。
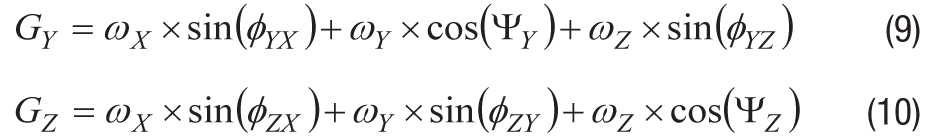
式8、9、10の両辺を積分すると、角変位に基づく同様の関係式が得られます。このように、各ジャイロスコープの出力の積分θXG、θYG、 θZGは、基準フレームに対する角変位θXω、θYω、θZωを使って表されます。
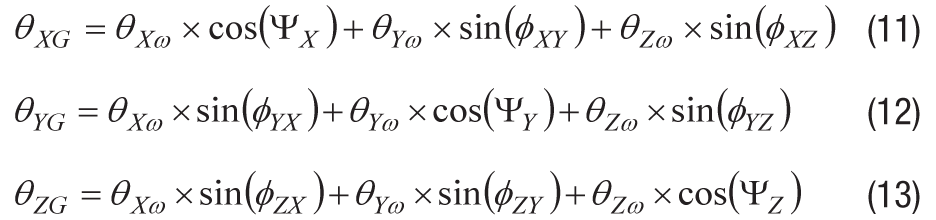
【例題2】
地上走行用の無人車両(UV:Unmanned Vehicle)があったとします。この車両はアンテナ用のプラットフォーム安定化制御(PSC:Platform Stabilization Control)システムを搭載しており、フィードバック・センサーとしてMEMS IMUを利用しているものとします。また、同システムはRSSチューナ・ループを搭載しており、連続通信を維持するために方位角と仰角を±1°以内に保つ必要があると仮定します。条件が動的に大きく変化する環境下で、PSCはY軸のジャイロスコープの測定値に応じて仰角を制御し、Z軸のジャイロスコープの測定値に応じて方位角を制御します。この場合、ミスアライメント誤差をどの程度に抑える必要があるでしょうか。 なお、この動的な条件下において車首方位θZωの最大変化量は30°で、動作中にX軸周りとY軸周りの回転は生じない(θXω=θYω=0)とします。
【解答】
X軸およびY軸周りの回転がないことから、式12と13は次のように簡素化されます。
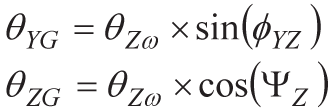
まずはY軸について、θYGの最大値を1°としてミスアライメント成分ΦYZを求めます。
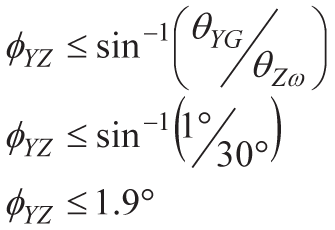
つまり、Y軸のジャイロスコープのミスアライメント誤差は最大1.9°まで許容できることになります。次に、Z軸についてはθZωを30°とし、θZGとθZωの差の最大値を1°としてΨZを求めます。この結果、Z軸のジャイロスコープのミスアライメント誤差は最大14.8°まで許容できることになります。
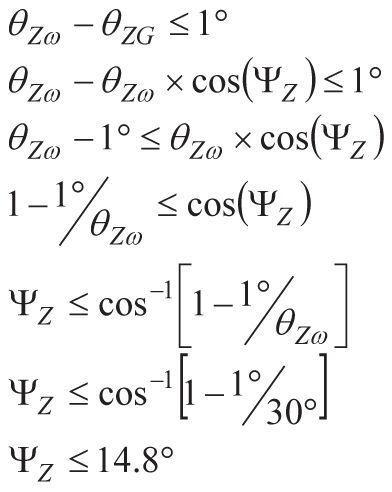
以上の結果から、この条件下においてY軸とZ軸の軸間の動作を維持するために、1.9°未満のアライメント精度が必要であることがわかります。
電気的なアライメント
IMUならびにそれを利用するシステムが、システムとして必須の目標を達成できない場合にはどうすればよいでしょうか。その場合、電気的なアライメントによってミスアライメント誤差を縮小することになります。この処理は主に2つのステップで構成されます。1つ目のステップでは、IMUを配備した後にミスアライメント成分の特性を評価します。2つ目のステップでは、アライメントを補正するための行列を求めます。この行列をジャイロスコープの配列に適用することで、基準フレームに沿って配置されている場合と同等の応答が得られるようにジャイロスコープを補正することができます。式14はこの処理のシステム・モデルです。

基準フレームにおける各軸周りの回転ω が3つのシステム入力です。また、3つのジャイロスコープの応答Gが3つのシステム出力です。3×3の行列Mは、入力と出力の間のシステムの動作(ミスアライメントを含む)を表します。簡単な代数演算を行うことにより、ジャイロスコープの測定値Gと行列Mの逆行列M-1の積が、基準フレームの回転配列ωに等しいことがわかります。つまり、アライメント行列はM-1に等しいということになります。

式8、9、10に基づいて、ミスアライメント成分が含まれるように式14を拡張すると式16が得られます。式17と式18は、それをより一般的に表現したものです。
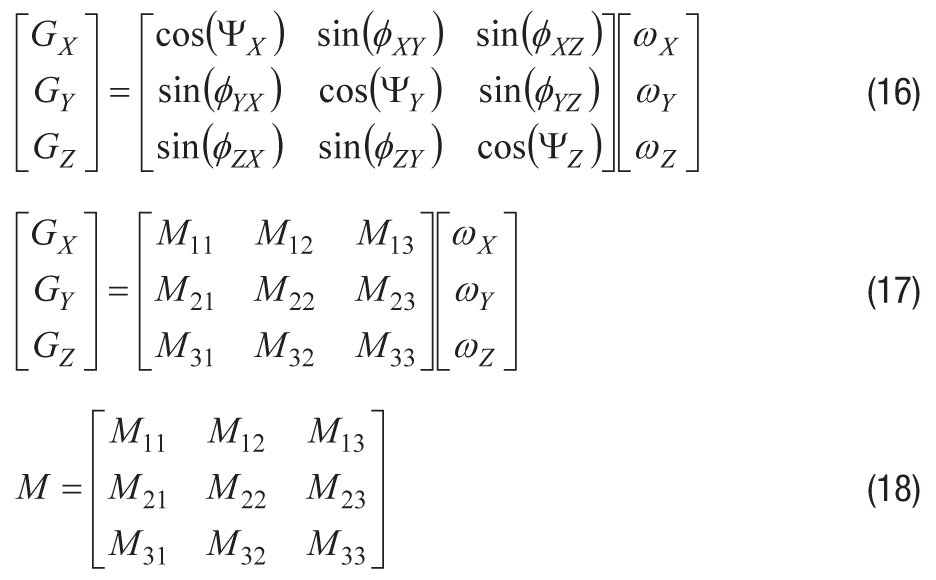
システム全体を一度に1つの軸周りに回転させると、システム・モデルが簡素化されます。この結果、1つのジャイロスコープの測定値を使って行列の各要素を分離することが可能になります。例えば、3つのジャイロスコープを観測しながら、システムをX軸の周りで回転(ωX=ωTR、ωY=0、ωZ=0)させると、M11、M21、M31の関係式は次のように簡素化されます。

同様に、Y軸の周りで回転(ωX=0、ωY=ωTR、ωZ=0)させると、M12、M22、M32の関係式は次のように簡素化されます。

最後に、Z軸の周りで回転(ωX=0、ωY=0、ωZ=ωTR)させると、M13、M23、M33の関係式は次のように簡素化されます。

明白なことですが、この処理には、モーション・プロファイルω とジャイロスコープの測定値Gの精度が直接的に影響を及ぼします。特に軸外の動きは、この処理に多大な影響を及ぼす可能性があるため、慣性テスト装置を 購入/導入する際には十分な考慮が必要になります 。また、ジャイロスコープについては、バイアスとノイズが精度を低下させる要因になるので、この処理に関する十分な検討が必要です。ジャイロスコープの測 定値における残余バイアス誤差bEの影響を制御するための1つの方法は、大きさが等しく方向が逆の異なる2種類の回転速度を用いることです。例えば、Y軸 周りを正の方向に回転(ωX=0、ωY=ωTR、ωZ=0)する場合、バイアス誤差を含むZ軸のジャイロスコープの応答は式28で表されます。Y軸周りを 負の方向に回転(ωX=0、ωY=-ωTR、ωZ=0)する場合、Z軸のジャイロスコープの応答は式29のようになります。

左辺がバイアス誤差bEとなるように式29を変形し、それを式28に代入するとM32が求まります。この式にはバイアス誤差bEが含まれていないことに注目してください。

ここで示した方法では、両方の測定においてバイアス誤差が一定であると仮定していますが、この仮定は現実的なものではありません。そこで、測定間に生じるばらつき(温度、時間、ノイズ)の可能性についても理解しておく必要があります。安定した温度条件の下で連続して測定が行われる場合には、ノイズがこの処理において管理すべき主要な誤差要因となります。ジャイロスコープによる測定で許容できるノイズのレベルは、アライメント精度の目標値ΨTと特性評価を行う際の各軸の回転速度ωTRに依存します。ノイズを低減するための一般的な手法として、一定の慣性条件の下でジャイロスコープによる測定を行った結果の時間平均をとる処理が挙げられます。アラン分散曲線を使用することによって、再現性(ノイズ)と平均化時間の間のトレードオフについて理解することができます。
【例題3】
特性評価を行う際の回転速度が100°/s、アライメント精度の目標値が0.1°、ノイズ(RMS値)がミスアライメントの目標値の1/10以下でなければならないとします。この目標を達成するためには、ADIS16485の出力をどれだけの時間、平均化すればよいでしょうか。
【解答】
ジャイロスコープと入力(テスト・プラットフォーム上での回転)の間の一般的な応答を用いて以下の計算を行います。この結果、各ジャイロスコープの総ノイズ(RMS値)は62°/hour未満でなければならないことがわかります。
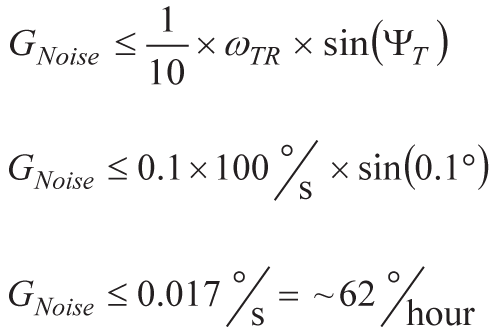
図6は、アラン分散曲線を用いて、このIMUに関する要件を満たすための平均化時間を導出する例です。ここでは、やや余裕を持たせて平均化時間を0.1sとします。これにより、62°/hourという再現性の目標値を十分にクリアすることができます。
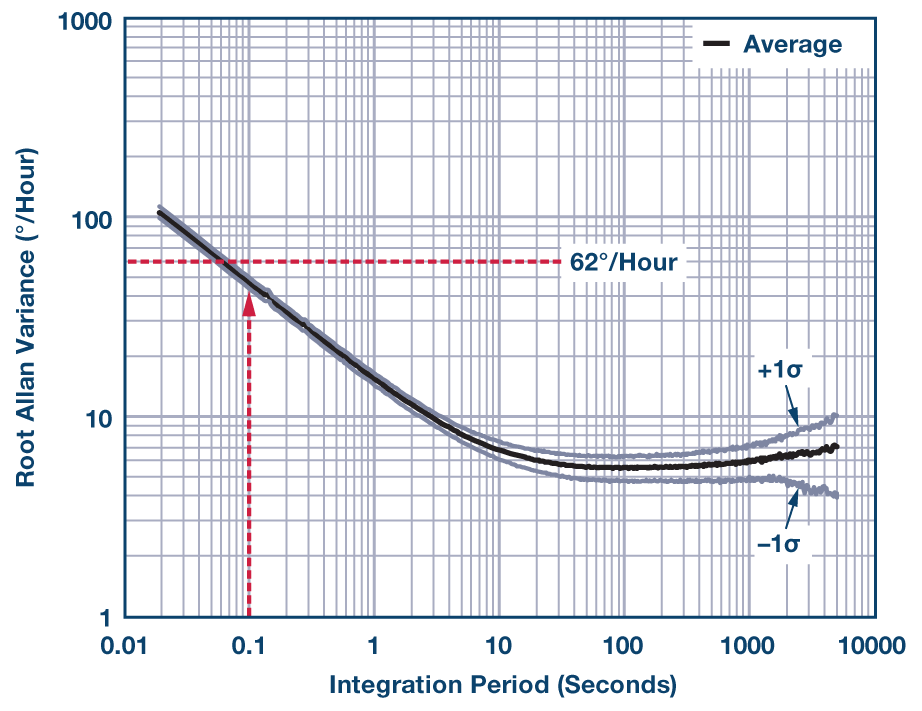
この方法では、センサー自体のノイズしか考慮していないことに注意してください。例えば、テスト・プラットフォームで振動が生じる場合、ジャイロスコープによる測定にさらにノイズが加わります。この結果、さらなる検討とフィルタリングが必要になる可能性があります。
処理を簡素化するためのヒント
温度環境の制御機能を備え、必要な精度を達成可能な3軸慣性テスト・システムを開発するために、資本設備と技術開発に必要なリソースに対してかなりの投資を行う必要があります。通常、第1世代、第2世代のシステムを開発している場合、その途中で多数の疑問点に遭遇するはずです。そうなると、十分なリソースや時間を確保できなくなる可能性もあり、その結果、シンプルなソリューションが必要になることもあります。しかし、そのようなソリューションを得るには、IMUを慎重に選定するとともに、計測器やアプリケーションにおける自然な動きも活用しなければなりません。
例えば、角度を扱う方が角速度を扱うよりも便利な場合があります。式31は、式11、12、13を組み合わせて、基準フレームに対する角度θXω、θYω、θZωと、ジャイロスコープの出力の積分θXG、θYG、θZGによってシステムの動作Mを表したものです。
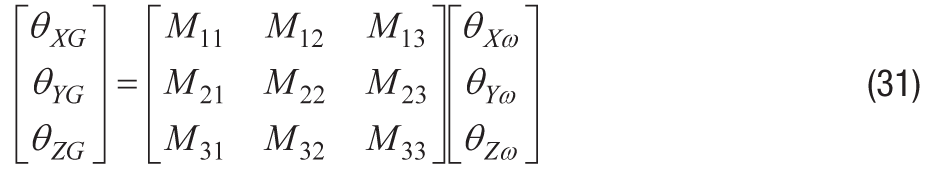
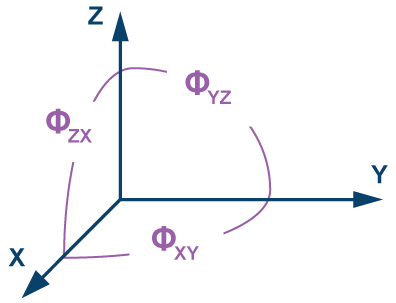
デバイスを選定する際には、軸間のミスアライメント誤差が重要な検討事項になります。それが軸とパッケージの間のミスアライメントの値よりも小さければ、電気的なアライメントに伴う(式16の)慣性テストのプロファイルの複雑さが軽減されるからです。軸とパッケージの間のミスアライメントは、外部の機械的基準に対するジャイロスコープの向きを表します。これに対し、軸間のミスアライメントは、他の2つのジャイロスコープに対する各ジャイロスコープの向きを表します。ほとんどの場合、MEMS IMUが備える3つのジャイロスコープは、互いに90°の角度をなすのが理想的です。軸間のミスアライメントは、軸間感度という別の共通パラメータに依存します。図7を基準にすると、軸間のミスアライメントは次の3つの関係式の最大値となります。

電気的なアライメントにおいて、軸間のミスアライメントは、センサーが互いに完全に直交して配置されているという仮定からのずれとなります。完全に直交するという仮定が成り立てば、3つの軸すべてを2つの回転軸だけで表すことが可能です。例えば、Y軸とZ軸の周りで回転させると、M12、M13、M22、M23、M32、M33を直接観測することができます。完全に直交して配置されると仮定して三角法に基づく性質を適用すると、これら6つの要素と以下の関係式から、他の3つの要素M11、M21、M31を算出することが可能です。
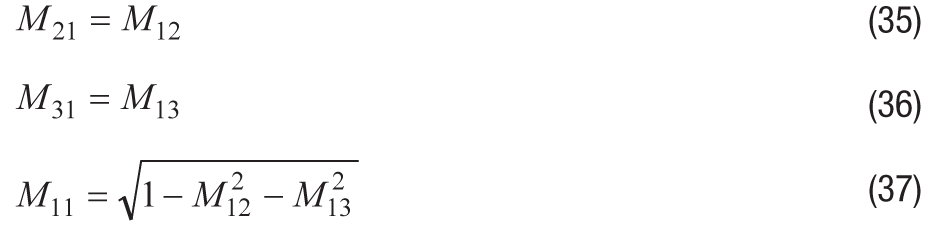
以上の式から、システム・モデルは次のように表すことができます。このように、行列Mの9つの要素が、Y軸とZ軸の回転によって得られた6つの要素で表現できています。
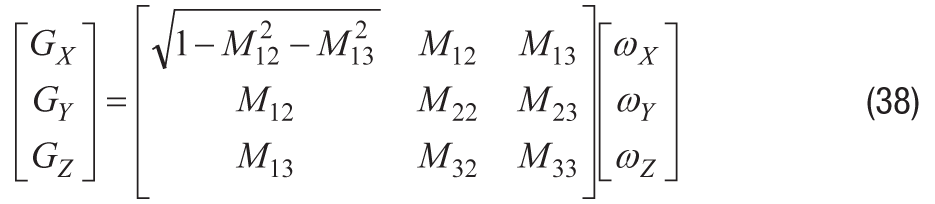
まとめ
MEMSをベースとする慣性技術は、ここ数年の間に飛躍的に進歩しました。その結果、サイズ、重量、消費電力、ユニット・コスト、統合コスト、性能を含む複雑なトレードオフにおいて、システム開発者に幅広い選択肢が提供されるようになりました。
MEMS IMUを用いたモーション制御システムを初めて設計する際、適切なIMUを選定し、そのIMUによってシステムに必須の要件を満たせるよう準備するために学ぶべき事柄が多数存在します。アライメント精度は、性能、コスト、スケジュールに関する必須の目標に多大な影響を及ぼす可能性があることから、重要な検討項目だと言えます。概念設計やアーキテクチャ設計の段階で潜在的なリスクを検出するうえで、簡単な解析ツールさえも役に立つことは少なくありません。その段階であれば、デバイスの選定、機械設計、組み立て後の校正(電気的なアライメント)、コストの事前見積もり、開発スケジュールを修正できる可能性があります。これをさらに一歩進めれば、MEMS IMUの主要な評価基準について理解し、3軸慣性テスト装置をシステム内の自然な動作で置き換える機会を認識することが、システムから最大限の価値(性能の向上や、配備にかかる総コストの削減)を得るために役立つということに気づかされるでしょう。

